HITCON CTF 2018 - Lost Modulus

Last weekend was HITCON CTF 2018, and it was really awesome! I personally spent time on various super interesting challenges. Below is just one of them that I happened to solve on the first day. I found to be particularly interesting to solve since I never have had a chance to dive into any homomorphic encryption systems before.

I lost my modulus. Can you find it for me?

nc 13.112.92.9 21701

crypto-33dee9470e5b5639777f7c50e4c650e3.py

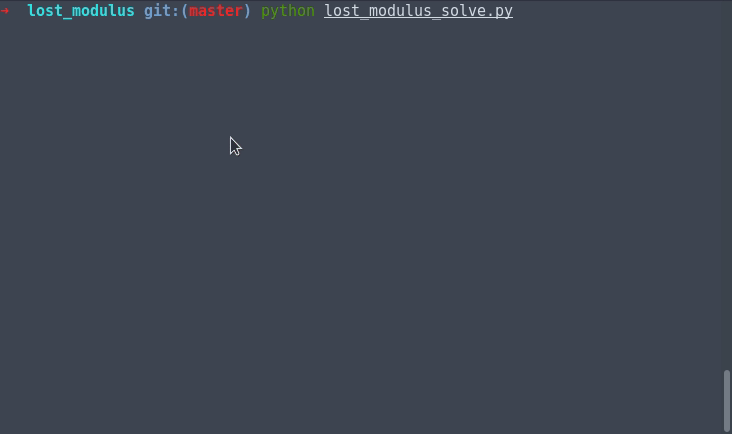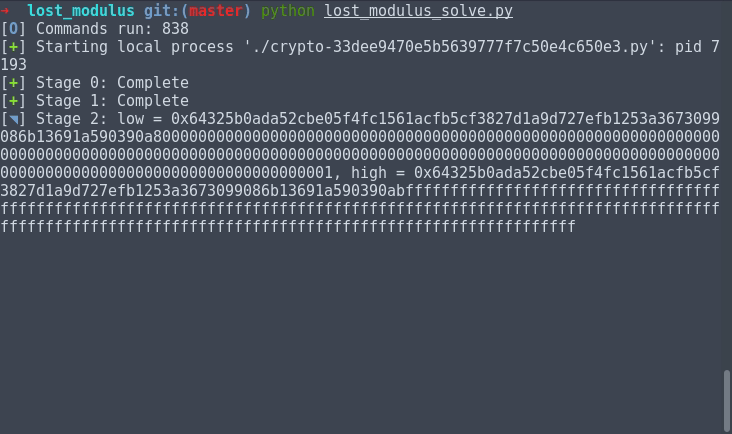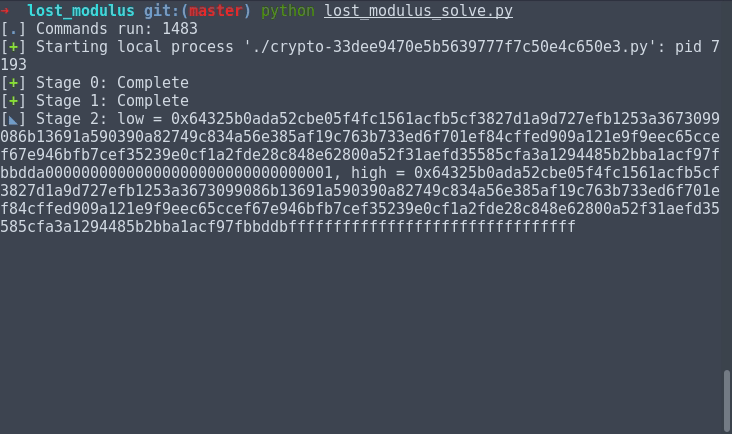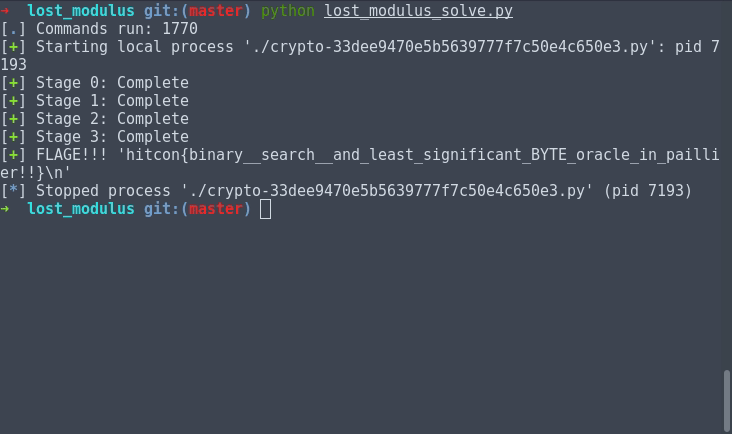
Simply because the attack has an almost movie-like decryption, here's a gif demo of my script before I start explaining things:

The server script seems to implement the Paillier Cryptosystem, and exposes the ability to perform some queries.

The server first gets two 512-bit primes p and q, and then proceeds to perform standard key-generation to compute required intermediates for encryption and decryption. One thing to note here is that since p and q are of equivalent length, the simpler variant for key generation is used, but otherwise it seems to be standard.

Once that is done, it encrypts the flag and sends it to us, and then exposes the ability to perform a maximum of 2048 queries. These queries can be one of two kinds A or B:

• A: Encrypt arbitrary input
• B: Decrypt arbitrary input, but only receive the least significant byte.

Upon reading the Wikipedia page for this cryptosystem, we realize that it is additive-homomorphic. This means that we can produce the encryption of any linear combination of messages, if we have the encrypted messages themselves. In particular D(E(m1) * E(m2)) == m1 + m2. This turns out to be extremely useful in solving this challenge.

Since we have the encrypted flag (which we'll call flag_enc), and we have a lsB (least significant byte) decryption oracle (query B), we can easily obtain the least significant byte of the flag. If we know modinv(256, n * n), we can repeatedly subtract out the least significant byte (since Paillier is additive-homomorphic), and then multiply by this value (which effectively divides it by 256), and then perform query B to obtain the entire flag.

However, we are not provided n by the server, hence the name of the challenge "Lost Modulus", we presume.

To find n, we considered a bunch of different approaches, two of which were msb (most significant bit) based leak, and binary search. We were unable to get the msb approach working, so we decided upon the binary search.

The binary search technique required usage of the fact that if we encrypted a value (say x) that was larger than or equal to n, and then decrypted it, then the least significant byte would not match up with x's least significant byte. However, if x was smaller than n, then it would match up. Notice that we require 2 operations for each query for the binary search here (A to encrypt, and B to get the lsB). Since n is 1024 bits long (as both p and q are 512 bytes each, and n = p * q), this would take 2048 queries.

And this is where we hit upon the query limitation. Within the number of queries that it would require to get n, we would no longer have any queries left to get the flag. Recall that n changes on each connection.

Recall that to get one byte of the flag, we require two operations (one to find out what value to subtract, and another to perform the decoding after the multiply). This meant that every 2 operations that we could shave off of the 2048 required for the binary search would give us 1 more byte of the flag.

The first 2 operations are easy to shave off: n must be odd (since p and q are odd, as they are large primes), which means that the lsb of n must be a 1. At this moment, we decided to write up a script to perform the attack.

Unfortunately, it took approximately half an hour (due to round trip times) to perform all the queries required to get n, which only revealed one byte of the flag. We could possibly parallelize this, except we need to know the "previous" byte of the flag to calculate the "current" byte, so it must happen one after another. We could possibly get around this issue, by calculating many ns together, while keeping open connections, waiting for previous bytes of the flag to be flushed, and then use them, however the server allowed only 4 concurrent connections. Due to the size of n, we knew that the flag could be upto 128 bytes, which meant even this was infeasible, so we decided to try to improve the query performance further.

We then started thinking about how we might do the binary search differently. Recall that Paillier is additive-homomorphic, which means if we pre-compute a table of encrypted values (using type A queries), and if some value we want to encrypt is a linear combination of these, then we can simply obtain it directly. This saves us on A type of queries. A good set of values to pre-fetch are powers of two, since we can simply look at the binary encoding of a number, except there are 1024 powers of 2, which are potentially smaller than n, which doesn't give us any savings.

However, we realize that we can simply pre-fetch (using type A queries) only some subset of them, using the fact that 2^(n+1) == 2^n, which can give us the rest of the values. We thus settled upon pre-fetching for 2^0, 2^2, 2^4, ... (which is a total of 512 queries). Notice that this save us 512 queries, which is more than sufficient to obtain the flag in a single connection.

When we implement this however, we faced an issue (which in hindsight should've been a non-issue, since we should've taken everything modulo n^2) but it took a long time to actually perform all the multiplies needed to get the encrypted form of a number with lots of 1s in its binary representation, in terms of CPU time. Recall that to add m1 and m2, in the encrypted world we need to multiply them. Thus, we decided to add in memoization, with a randomized fetching via a type A query, for about 10% of the numbers that we wanted to encrypt. Overall, this meant that although we were making more queries, we would be able to get values much faster.

Overall, our script finds the flag in approximately 1700~1800 queries.

Explanation of Script

Query Setup

This part simply imports all important libraries, and sets up two extremely useful helper functions cmdA and cmdB that can be used to quickly perform queries. It also sets up a global running counter of number of queries used (which during the CTF, we called "commands run"). This made it easy for us to diagnose how things are going while it is running.

from pwn import *
from Crypto.Util.number import *
from gmpy import *
from os import getenv
from random import random


commands_run = 0
commands_run_prog = log.progress("Commands run")


def cmd(c, inp):
    global commands_run
    commands_run += 1
    commands_run_prog.status(str(commands_run))
    conn.recvuntil("cmd: ")
    conn.sendline(c)
    conn.recvuntil("input: ")
    conn.sendline(long_to_bytes(inp).encode('hex'))
    return bytes_to_long(conn.recvline().strip().decode('hex'))

Stage 0

Here, we set up the connection to the server, and get the encrypted flag flag_enc.

def stage0():
    global conn, flag_enc
    if getenv('LOCAL') != "TRUE":
        conn = remote('13.112.92.9', 21701)
    else:
        conn = process(
            './crypto-33dee9470e5b5639777f7c50e4c650e3.py'
        )
    conn.recvline()
    flag_enc = conn.recvline().strip()
    flag_enc = bytes_to_long(flag_enc.decode('hex'))
    log.success("Stage 0: Complete")

Stage 1

Now, we have to prime up the encode function by pre-fetching the requisite data. We additionally set up a separate encode function which uses the pre-fetched memo, in order to reduce the number of queries required. It also performs cmdA with 10% probability, to speed up encryptions as mentioned above.

memo = {}


def stage1():
    global memo
    prog = log.progress("Stage 1")
    for i in xrange(1024):
        prog.status(str(i))
        if i % 2 == 0:
            val = cmdA(2 ** i)
        else:
            prev = memo[2 ** (i - 1)]
            val = prev * prev
        memo[2 ** i] = val
    prog.success("Complete")


def encode(inp):
    global memo
    if random() < 0.1:
        memo[inp] = cmdA(inp)
        return memo[inp]
    val = None
    inp_copy = inp
    for k in sorted(memo.keys())[::-1]:
        while k <= inp:
            if val is None:
                val = 1
            val *= memo[k]
            inp -= k
    memo[inp_copy] = val
    assert inp == 0, repr(inp)
    return val

Stage 2

Now, we move on to actually computing the value of n. This is a relatively standard binary search, with minor modifications to ensure that we are only looking at odd numbers.

def stage2():
    global n
    checks = 0
    low = 0
    high = 2**1023
    prog = log.progress("Stage 2")
    while low <= high:
        mid = (low + high) // 2
        checks += 1
        prog.status("low = %s, high = %s" %
                    (hex(low), hex(high)))
        test = mid * 2 + 1
        y = cmdB(encode(test))
        x = test % 256
        if x != y:
            high = mid - 1
        elif x == y:
            low = mid + 1
        else:
            assert False
    prog.success("Complete")
    n = low * 2 + 1

Stage 3

Now that we have n, we have to compute the flag.

def stage3():
    global flag
    shifter = invert(256, n * n)
    known_flag = []
    prog = log.progress("Stage 3")
    for lsh in xrange(128):
        assert lsh == len(known_flag)
        val = flag_enc
        prev_lsh = lsh - 1
        subtr_val = 0
        while prev_lsh >= 0:
            prev = known_flag[prev_lsh]
            subtr_val *= 256
            subtr_val += prev
            prev_lsh -= 1
        if lsh > 0:
            neg = ((n * n) - subtr_val) % (n * n)
            val = val * cmdA(neg)
        test = pow(val, shifter ** lsh, n * n)
        known_flag.append(cmdB(test))
        if known_flag[-1] == 0:
            break
        prog.status(repr(''.join(map(chr, known_flag))[::-1]))
    flag = ''.join(map(chr, known_flag))[::-1].strip('\0')
    prog.success("Complete")

Profit

We call out all the stages in order, and profit with a flag!

stage0()
stage1()
stage2()
stage3()
log.success("FLAGE!!! " + repr(flag))

Flag

hitcon{binary__search__and_least_significant_BYTE_oracle_in_paillier!!}

I originally wrote this for the PPP public-writeups repository. Adapted it with minor stylistic changes for the blog.